图论基础概念

1.1 什么是图

我们首先需要知道什么是图，才能开始讨论图的性质和算法。这里说的图是一幅像梵高画的《星空》那样的图画么？还是百度地图呢？都不是，那它是什么呢？

图论起源于著名的哥尼斯堡七桥问题。

在哥尼斯堡的普莱格尔河上，有七座桥将河中的两座岛与两边河岸联结起来，问题是能否从这四块陆地中任何一块开始，通过每一座桥正好一次，最后回到起点。

这个问题你知道如何解决么？欧拉在 1736 年解决了这个问题，他用抽像分析法将这个问题化为第一个图论问题：即把每一块陆地用一个点来代替，将每一座桥用联接相应的两个点的一条线来代替，从而相当于得到一个“图”（如下图）。

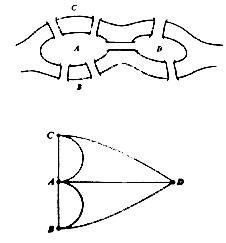
图 1.1 七桥问题

因此我们按如下方式定义一张图：

图 G=(V, E)，其中 V={vi} 表示图上的点集，其元素称之为顶点，E={<vi-vj>| vi, vj in V} 表示顶点与顶点之间关系的边集，图 G 就是 E 和 V 的二元组。

对于七桥问题，有点集 V={A, B, C, D}，边集 E={<A-B>1, <A-B>2, <A-C>1, <A-C>2, <A-D>, <B-D>, <C-D>}（<x-y> 表示点 x 和点 y 之间存在一条路）。

1.2 无向图和有向图

无向图：在一个图中，如果它的任意一条边是无方向的，即对于边 <x-y>，x 和 y 可以通过该边互相到达，那么称这个图为无向图，称无方向的边为无向边。通常来说公交线路及其站点就是一个无向图，可以从站点 A 到达站点 B，也可以通过同样的路从 B 到达 A。
有向图：在一个图中，如果它的任意一条边是有方向的，就像城市中的单行道，那么这个图就是有向图。
混合图：既有有向边也有无向边的图，这是一种特殊的图。

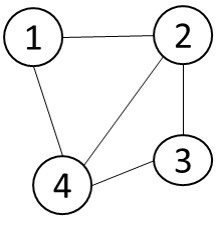
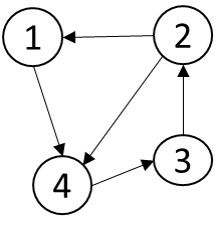
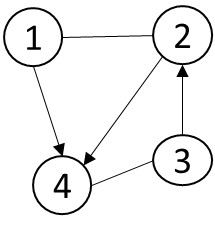
图 1.2 从左至右分别为无向图、有向图及混合图

1.3 图的储存结构

一般对于一个图 G=(V,E)，我们有两种常用方法来储存（表示），即邻接矩阵法和邻接表法。

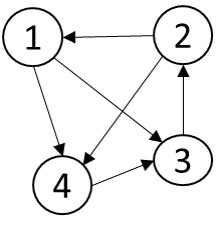
图 1.3 示例图 G1

邻接矩阵法：

在邻接矩阵表示法中，我们用一个 V*V 的矩阵 A 表示顶点之间的相连关系。通常把 A(i,j) 设为 0 或者无穷大（inf）表示不存在边 <i->j>，否侧，A(i,j) 即说明存在边 <i->j>，并且其值就是边<i->j> 的权值。对于无向图，邻接矩阵 A 是一个对称矩阵。一个图的邻接矩阵表示，需要占用 O(V*V) 的储存空间，与其边数无关。

这种表示方法的不足在于对于一个 |E|<<|V*V| 的稀疏图，它的空间消耗会比邻接表表示大很多，同时它无法保存重边。

下图说明图 G1 如何在邻接矩阵中存放的。
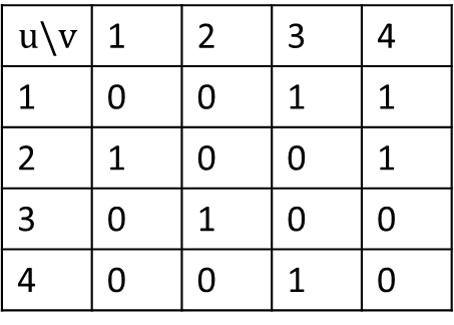
邻接矩阵法
图 1.4 图 G1 的邻接矩阵表示法

邻接表法：

我们用 |V| 个链表表示图 G，对于 V 中的任意一个顶点 v，都对应一个表头元素为 v 的链表，该链表表头之后紧接着的元素 u 都满足 <v->u> in E。

邻接表法
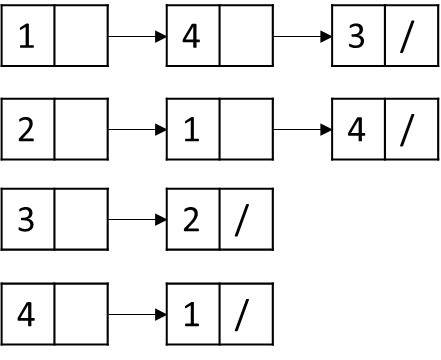
图 1.5 图 G1 的邻接表表示法

习题 1.3 将要求读者采用链表这一数据结构编程实现图的邻接表示。

以下代码是用数组对邻接表的模拟，以后章节大部分的图都将采用这种方式表示：

int head[MAXN]; // 从i点出发的最后一个子节点的位置
struct node{
	int cur,pre,weight;//cur当前节点标号，pre前一个兄弟节点位置，weight表示边<from->cur>的权重
} edge[MAXN];
int cnt;//边数

void initEdge() { // 初始化边
	cnt = 0;
	for(int i = 0; i < MAXN; i ++)head[i] = -1;
}

void addEdge(int from, int cur){ // 加入新的边
	edge[cnt].cur = cur;
	edge[cnt].pre = head[from];
	head[from] = cnt ++;	// head值更新为当前顶点位置
}

void print(int v){
	// 依次访问顶点v的邻接顶点
	for(int i = head[v]; i != -1; i = edge[i].pre) {
		int cur = edge[i].cur;
		printf("%d ", cur);
	}
}

1.4 度

对于顶点 i，我们把顶点 i 所邻接的边数称之为顶点 i 的度，记为 deg(i)，其中指向顶点 i 的边数称之为入度，记为 id(i) ，类似的，顶点 i 有出度，记为 od(i)。

对于图 G=(V,E)，总有 deg(i) = |id(i)| + |od(i)|。
对于无向图，总有 |id(i)| = |od(i)|。

拓扑排序

大学某些课程是有先修关系的，比如学习数据结构之前必须先学C语言，学习数值分析之前要先学高等数学和线性代数等等。那么给定课程之间的先修关系，如何得到一个合法的课程学习顺序，即使得对于任意一门课程y，其先修课程都排在它的前面。

首先我们对这个问题形式化，对有向图 G=(V,E) 进行拓扑排序后，拓扑序列，满足对于所有有向边 <a->b>，a 都在 b 的前面。

思考以下两幅图是否存在拓扑序列。

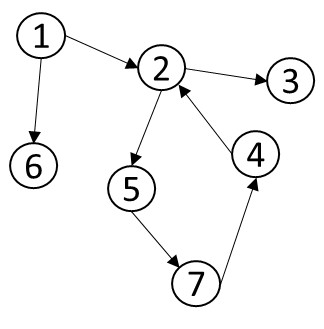
图1.4
图1.4

图1.5
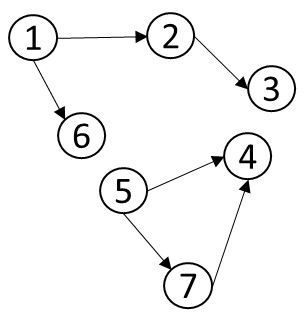
图1.5

定理 1.1：

一个存在拓扑序列的图，必然是一个有向无环图。

对于该定理，此处不做证明。

我们将通过以下算法步骤解决该问题：

计算所有顶点的入度；
将入度为 0 的顶点 u 及其邻接的边从图中删除，并将该顶点 u 加入已排序序列。入度为 0 的顶点 u 说明此时图中不存在有向边 <v->u> 使得另一顶点 v 排在 u 前面；
重复步骤 1、2，直至不存在入度为 0 的顶点；
如果此时图中还存在顶点，那么剩下的顶点及边将形成至少一个回路，出现矛盾，所以原图不存在拓扑序列；如果图中无顶点，那么已排序序列即为所求拓扑序列，算法结束。

代码：

int sortlist[1000];
int topsort(){
	queue<int> q;
	int idx = 0;
	for(int i = 0; i < n; i ++){//n为要排序的顶点个数
		if(indgree[i] == 0){
			q.push(i);
		}
	}
	while(q.empty() == 0){
		int cur = q.front();
		sortlist[idx++] = cur;
		q.pop();
		n--;

		for(int i = 0; i < l[cur].size(); i ++){
			// l[cur][i]表示以cur为起点i为终点的有向边
			indgree[l[cur][i]] --;
			if(indgree[l[cur][i]] == 0){
				q.push(l[cur][i]);
			}
		}
	}
	if(n > 0) return 0;   // 当n>0时，说明有节点未排序则表示节点关系有冲突
	return 1;
}

欧拉图

我们在 1.1 节提出了七桥问题。七桥问题的一般形式是一笔画问题，对于一个图 G=(V,E)，我们是否能从某点开始，经过所有边仅一次。如果能，那么我们称该路径为欧拉路径。同时将最后回到起点的欧拉路径称之为欧拉回路，那么称存在欧拉回路的图为欧拉图。对上题进行简化可知，就是判断欧拉图并输出欧拉路径。

如何判断一个图是否存在欧拉路径？
如何判断一个图是不是欧拉图呢？

为解决以上两个问题，首先我们必须要将不连通的图排除，因为不连通的图肯定不存在欧拉路径，如图 1.6 所示.

图1.6
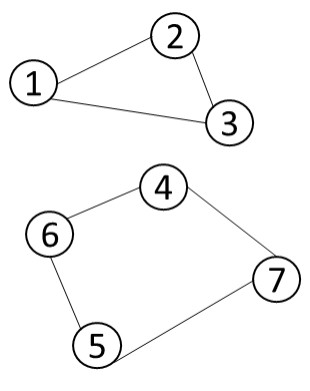
图 1.6 非连通图

思考下面这幅图是否存在欧拉路：

图1.7
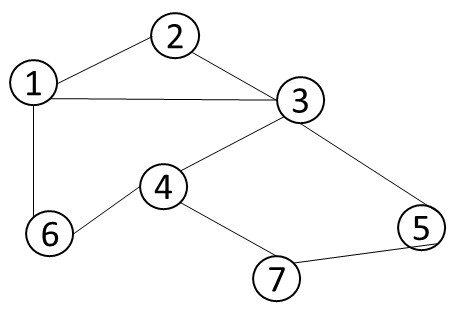
图 1.7 判断是否为欧拉图

我们将连通图简单地分为无向连通图和有向连通图进行分类讨论。

定理 1.2：

无向连通图 G 存在欧拉路径的充要条件：G 上所有顶点的度数为偶数，或者只有 2 个顶点度数为奇数。
无向连通图 G 是欧拉图的充要条件：G 中每个顶点的度都是偶数。

图1.8
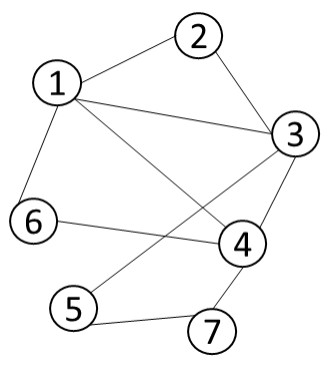
图 1.8 无向欧拉图

定理 1.3：

有向连通图 G 存在欧拉路径的充要条件：每个顶点入度等于出度；或者只有 1 个顶点入度比出度小 1，只有 1 个顶点出度比入度小 1，并且其他点入度等于出度。
有向连通图 G 是欧拉图的充要条件：每个顶点入度等于出度。

图1.9
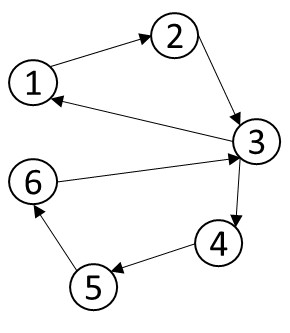
图 1.9 有向欧拉图

习题

1.1 节我们描述过七桥问题。
1. 七桥问题是否有解？如果有解，请画出解在图上的路径。
2. 对于混合图，如何求解其欧拉回路？
对于图的两种储存结构，删除一条边，分别需要多少时间？删除一个顶点，分别需要多少时间？
请采用链表这一基础数据结构，编程实现图 G 的邻接表表示。
在 1.4 节，有同学提出，也可以利用并查集对有向图的回路（环）进行检测，即在加入有向边 <a->b> 之前，a，b 两顶点在同一集合，那么 a，b 两点就在一个回路上。请举例证明这种想法是错误的。
请在 hdu oj 上编程解决以下题目：
- 1285 确定比赛名次
- 2094 产生冠军
- 2647 Reward
- 3342 Legal or Not
- 1811 Rank of Tetris
- 3231 Box Relations
- 1878 欧拉回路
- 3018 Ant Trip
- 1116 Play on Words
- 2894 DeBruijin
- 1956 Sightseeing tour
- 3472 HS BDC

2014/11/07